카메라 렌즈의 조리개 값 F-stop 과 수광량에 따른 수치변화
카메라 렌즈의 조리개 변화에 따른 수광량을 계산하는 기본적인 원리는 조리개 값(f-stop)이 변할 때마다 수광량이 1/2로 감소하는 것입니다. 여기서 조리개 값은 루트2 (약 1.414)의 배수로 변화하기 때문에, 조리개 값이 한 스톱 변할 때마다 수광량은 절반이 됩니다.
조리개 값의 변동 수치는?
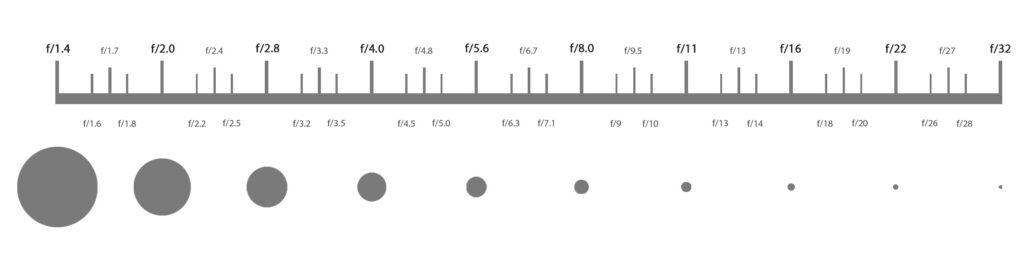
조리개 값은 f/1, f/1.4, f/2, f/2.8, f/4, f/5.6, f/8, f/11, f/16, f/22, f/32 으로 분류되며 보통 스탑 씩 기준으로 잡는다.
카메라에서 컨트롤 가능한 F값의 변화는 보통 1/3 스탑 씩 움직이기 때문에 익숙한 F값들은 아래와 같다.

조리개 직경은 매번 1/√2 값 수치로 줄어들기 때문에 실제로 빛을 받아들이는 수광량은 1스탑/1stop 당 절반으로 줄어든다. 결국 이러한 조건들을 기반으로 계산하면 아래와 같은 수광량 변화를 확인할 수 있다.
조리개 값 변화에 따른 수광량 변화 공식
- 조리개 값(f-stop)이 1스톱 커지면 수광량은 1/2배로 줄어든다.
- 조리개 값(f-stop)이 1스톱 작아지면 수광량은 2배로 증가한다.
예시: 수광량 계산
- f/1에서 f/1.4로 변화
- f/1 → f/1.4 (조리개 값이 한 스톱 커짐)
- 수광량은 1/2배 감소, 즉 100% → 50%
- f/1.4에서 f/2로 변화
- f/1.4 → f/2 (조리개 값이 한 스톱 커짐)
- 수광량은 1/2배 감소, 즉 50% → 25%
- f/2에서 f/2.8로 변화
- f/2 → f/2.8 (조리개 값이 한 스톱 커짐)
- 수광량은 1/2배 감소, 즉 25% → 12.5%
- f/2.8에서 f/4로 변화
- f/2.8 → f/4 (조리개 값이 한 스톱 커짐)
- 수광량은 1/2배 감소, 즉 12.5% → 6.25%
- f/4에서 f/5.6로 변화
- f/4 → f/5.6 (조리개 값이 한 스톱 커짐)
- 수광량은 1/2배 감소, 즉 6.25% → 3.125%
이와 같은 방식으로 수광량은 조리개 값이 커질 때마다 절반 씩 변화한다.
조리개 변화에 따른 수광량 표
| 조리개 값 (f-stop) | 상대적 수광량 (%) |
|---|---|
| f/1 | 100% |
| f/1.4 | 50% (1/2) |
| f/2 | 25% (1/4) |
| f/2.8 | 12.5% (1/8) |
| f/4 | 6.25% (1/16) |
| f/5.6 | 3.125% (1/32) |
| f/8 | 1.5625% (1/64) |
| f/11 | 0.78125% (1/128) |
| f/16 | 0.390625% (1/256) |
| f/22 | 0.1953125% (1/512) |
조리개 값이 커질 때마다 (수치가 커질수록/조리개를 조일수록) 렌즈를 통과하는 빛의 양은 절반씩 감소한다.
자연수√값 계산에 따른 조리개 값 및 상대적 수광량 (자연수버전)
| 자연수 (루트√) | 조리개 값 (f-stop) | 상대적 수광량 (단위 %) |
|---|---|---|
| 1 | f/1 | 100 |
| 2 | f/1.414 | 50 |
| 3 | f/1.732 | 33.33 |
| 4 | f/2 | 25 |
| 5 | f/2.236 | 20 |
| 6 | f/2.449 | 16.67 |
| 7 | f/2.646 | 14.29 |
| 8 | f/2.828 | 12.5 |
| 9 | f/3 | 11.11 |
| 10 | f/3.162 | 10 |
| 11 | f/3.317 | 9.09 |
| 12 | f/3.464 | 8.33 |
| 13 | f/3.606 | 7.69 |
| 14 | f/3.742 | 7.14 |
| 15 | f/3.873 | 6.67 |
| 16 | f/4 | 6.25 |
| 17 | f/4.123 | 5.88 |
| 18 | f/4.243 | 5.56 |
| 19 | f/4.359 | 5.26 |
| 20 | f/4.472 | 5 |
| 21 | f/4.583 | 4.76 |
| 22 | f/4.690 | 4.55 |
| 23 | f/4.796 | 4.35 |
| 24 | f/4.899 | 4.17 |
| 25 | f/5 | 4 |
| 26 | f/5.099 | 3.85 |
| 27 | f/5.196 | 3.7 |
| 28 | f/5.292 | 3.57 |
| 29 | f/5.385 | 3.45 |
| 30 | f/5.477 | 3.33 |
| 31 | f/5.568 | 3.23 |
| 32 | f/5.657 | 3.13 |
| 33 | f/5.745 | 3.03 |
| 34 | f/5.831 | 2.94 |
| 35 | f/5.916 | 2.86 |
| 36 | f/6 | 2.78 |
| 37 | f/6.083 | 2.7 |
| 38 | f/6.164 | 2.63 |
| 39 | f/6.245 | 2.56 |
| 40 | f/6.325 | 2.5 |
※굵은 글씨는 1/3 Stop 표시
상대적 수광량: 상대적 수광량은 f/1 조리개 값을 기준으로 100%로 계산했으며, 조리개 면적은 f-stop 값의 제곱에 반비례한다. 수광량은 루트값에 반비례하게 된다.
실제 카메라 조리개 값은 위 표처럼 소수점 아래로 상세하게 표시되지 않고, f/1, f/1.4, f/2, f/2.8 등과 같이 표준화된 값으로 표현됩니다. 위 표는 조리개 값과 수광량의 관계를 이해하기 위한 단순히 이론적인 정수값이다.

이 너무나도 당연한 글을 쓴 이유는.
조리개 값의 수치 변화와 수광량 에 대한 계산은 단순히 원형지름에 따른 루트 계산만 할 줄 알면 나오는 기본적인 계산이기 때문입니다.
그런데 어떻게 해야 수광량이 F1.2는 88%, F4는 60% 라는 얘기가 나오는 것인지.
설마 100 을 기준으로 F4 (40%) 빼서 60% 가 수광량이다! 하는 겁니까.
그럼 F9.9 에서는 센서 수광이 1% 라는 계산이고, F10에서는 빛이 0% 이라는 계산이 나오고
F11 이나 F16 에서는? F64 에서는 값이 마이너스가 되는데. 어디 블랙홀도 아니고 빛이 센서에서 빠져나가는 것도 아니잖습니까..

조리개가 낮다고, 밝게 촬영해서 선예도와 해상도가 맑은 것도 아닙니다.
조리개를 낮출 수 있는 것은
렌즈 가공 할 때 = × 틀림
렌즈수차 등을 줄일 수 있게 정밀 가공 하였기 때문에 = × 틀림
손실이 적어져서 밝은 렌즈입니다. = × 틀림
그럼 80년 전 소련제 F1.4 렌즈들은 다 선예도가 좋고 해상도가 좋습니까.
F0.3 , F0.7렌즈가 단순히 정밀가공도, 선예도나 해상도가 좋은 것도 아니잖아요.


